
The Round #1 exam for the 2017-2018 Academic Year will be held on:
** The 3-4pm option is offered for students who may have a schedule conflict with the earlier 2-3pm time slot. Contest rules specify that no student may begin the contest exam after any student has left the test room. Thus students who choose to take the exam during the earlier 2-3pm time slot must commit to staying until at least 3:05pm ... and students who chose the second time slot must arrive no later than 3:05pm!
Please Note: Students who think they may want to leave before 60 minutes are up should take the exam with the 3-4pm cohort!!
FURTHER INFO: Participants have exactly 60 minutes to work on the exam. Students should try to arrive on the hour (and no later than 5 minutes after). It takes about 10 minutes or more to distribute the exams and read through the instructions, so participants in the cohort beginning at 2pm should plan to be present from 2:00-3:15 pm.
You can have a look now at the exam instructions and answer sheet. At the beginning of each contest exam, we'll read through the instructions and you'll fill in the student information on the answer sheet...after that you'll have 60 minutes to work on the contest problems.
The AMATYC "Student Math League" Contest is a math contest held each year at community colleges nationwide. It consists of two one-hour exams. At CCSF, the first exam is typically given in early November and the second exam is given in early March. Each exam consists of 20 multiple choice questions covering precalculus material (e.g. algebra, geometry, trigonometry, and statistics/probability). Examples of past exams can be downloaded (as PDF files) from this AMATYC webpage. [Note: You'll need the free Adobe Acrobat software to read these files.] Various contest scholarships and prizes are awarded, among them:
All CCSF students are welcome to participate. No special registration is required --- all an interested student needs to do is come to the contest room at the announced time on the contest date. Students are also permitted to bring and use any scientific or graphics calculator that does not have a QWERTY (i.e. typewriter) keyboard.
Note, however, that students who have already earned a two-year college degree (or higher) are not eligible to compete for official awards.
If you'd like to learn more about the contest, you can:
or you may contact one of the following CCSF math faculty:
| Date | Time | Room | Instructor | |
|---|---|---|---|---|
| Pre-Contest Workshop |
|
| ||
| Pre-Contest Workshop |
|
|
||
| AMATYC Contest Exam: Round #1 |
|
(or 3:00–4:15 pm) |
Batmale 711 |
|
| Post-Contest Meeting |
|
|
During the pre-contest workshops we typically discuss how the contest works, look at problems from previous contest exams, and discuss solutions and strategies to help prepare students for the upcoming contest exam.
During the post-contest meeting we'll:
For other potential practice problems see:
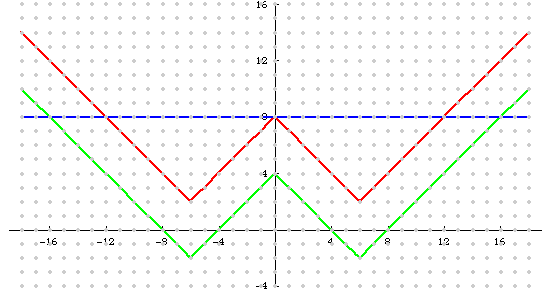
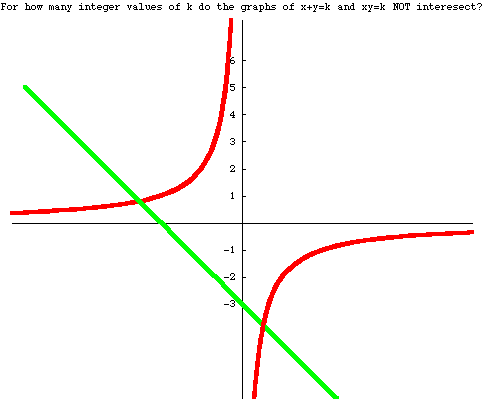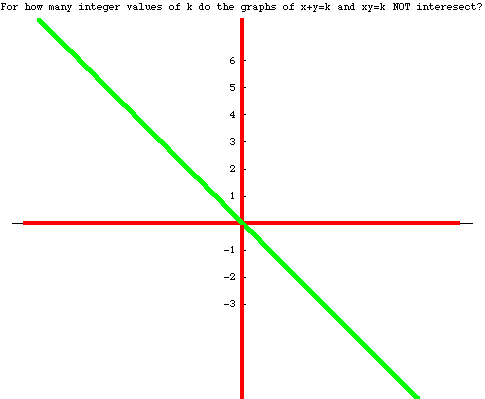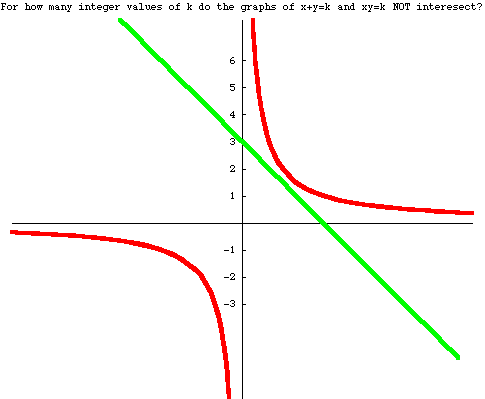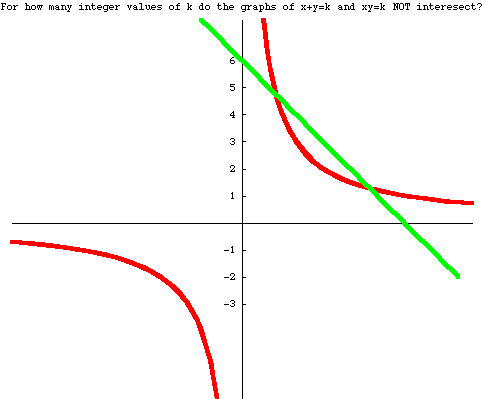
Find the value of k for which the equation |k – | |x| - 6| | = 2 has exactly 5 solutions.
(Can you see how the graphic below relates to this problem?)