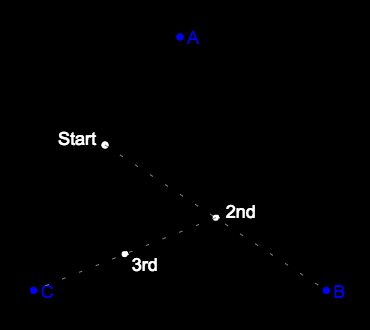
Suppose we are given the vertices of a triangle; call them A, B and C.
We then pick a starting point anywhere on the page (whether inside or outside the triangle doesn't matter) and place our first dot there.
To place the next dot, we randomly choose one of the vertices, let's say B in this case, and put the second dot halfway between our starting dot and B.
Then, we again randomly choose a vertex, let's say C this time, and put the third dot halfway between the second dot and C.
We proceed likewise for the fourth dot and so on.