........OVERVIEW
Chapter 16 - Constrained Motion of a Rigid Body

For some problems involving rigid bodies, we can find a kinematic relationship between the angular acceleration, α, and the linear acceleration of a point on the body, aP.

                                                                         

Centroidal rotation
A wheel rolling about its mass center without slip
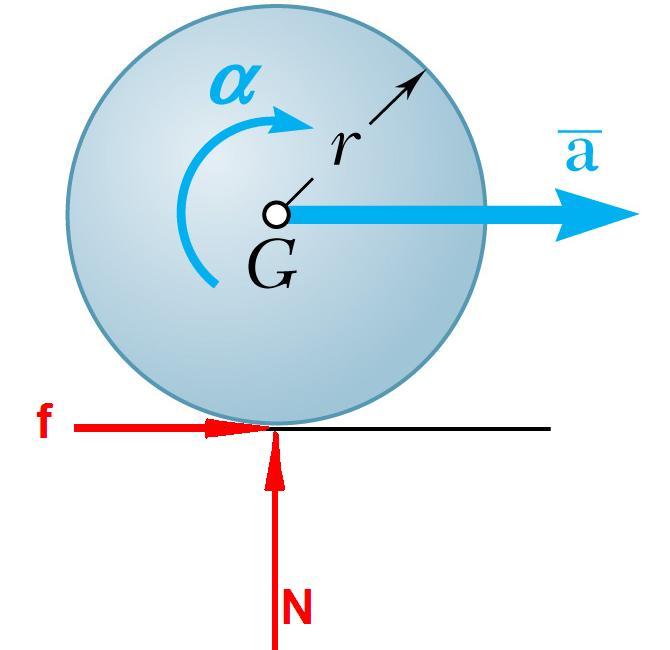
wheel rolling with linear acceleration of mass center G shown and also angular acceleration of wheel, alpha, shown
The kinematic relationship between the linear acceleration of the mass center and the angular acceleration of the body is:
aG = αr
The linear acceleration of any other point on the body can be calculated:
aP = aG + aP/G =  aG + [α x rP/G]  + [ω x (ω x rP/G)]
Also note that the frictional force at the floor will have to be static friction:
fs <= μsN

For a wheel rolling with slip there is no relationship between α and aG.

However, the frictional force at the floor will have to be kinetic friction:

fk = μkN
             
                

Noncentroidal rotation

A wheel rolling about a point not its mass center without slip

wheel whose center of gravity is not the geometric center rolling with linear acceleration of mass center G shown and also angular acceleration of wheel, alpha, shown

If the geometric center, 0, is not the center of gravity, then it will have this kinematic relationship:

aO = αr
And:
aG   = aO + aG/O
= aO + aG/Ot + aG/On
= aO + [α x rG/O ] + [ω x (ω x rG/O )]

             
               
A rigid body in pure translation
If there is no rotation of the body about its mass center, then
α = 0
                   
               
A rigid body in pure rotation
If there is no translation of the body, then
a = 0