Property Averaging of Composites
Let's graph the two expressions that we got for the two cases of isostress and isostrain.
The plot shown here is for the specific case of E-glass reinforced epoxy.
The top curve shows the case of isostrain:
Ec = VmEm + VfEf
The bottom curve shows the case of isostress:
Ec-1 = Vm Em-1 + VfEf-1
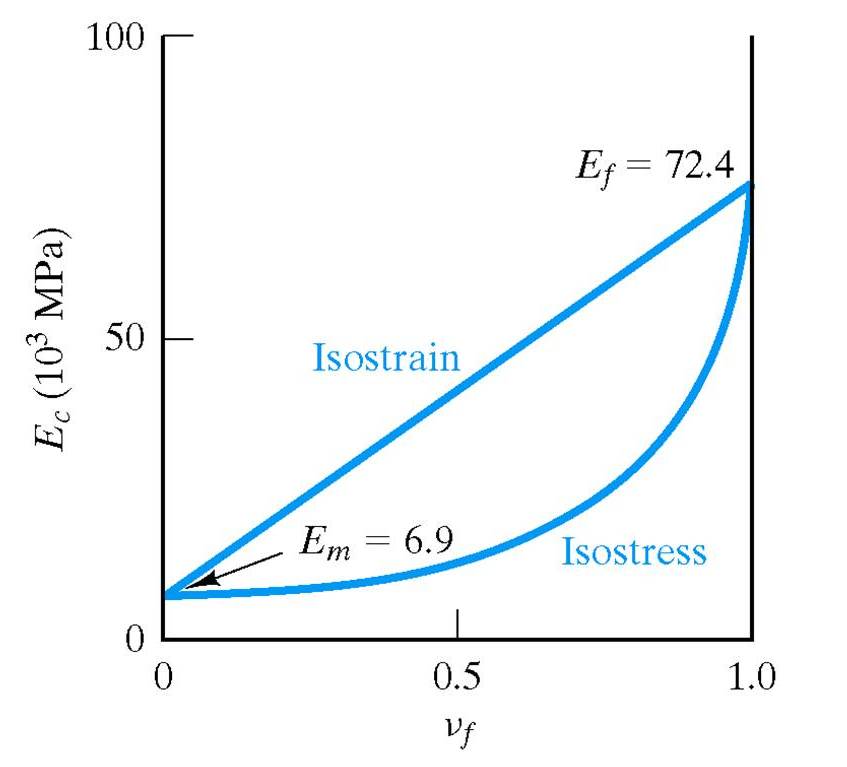
In the case of isostrain, the modulus of the composite varies linearly with the volume fraction of fibers. i.e. it is a weighted
average of the moduli of the matrix and fiber phases. We can see that for this case of parallel loading, the fibers make a greater
contribution to Ec than they do in isostress (perpendicular) loading. In the isostress case the modulus of the composite is dominated
by the modulus of the matrix except for very high fiber volumes.
Anything
other that isostrain or isostress can be a very complex
analysis. It will depend on specific nature of disperse and
continuous phases.
Question:
So how will we calculate the property of a composite for something other than these conditions?
Answer:
Let's consider that isostrain and isostress are two extreme ends
of a spectrum of geometries. Then we can assume that the property of any
composite, Xc, can be calculated from an equation like this:
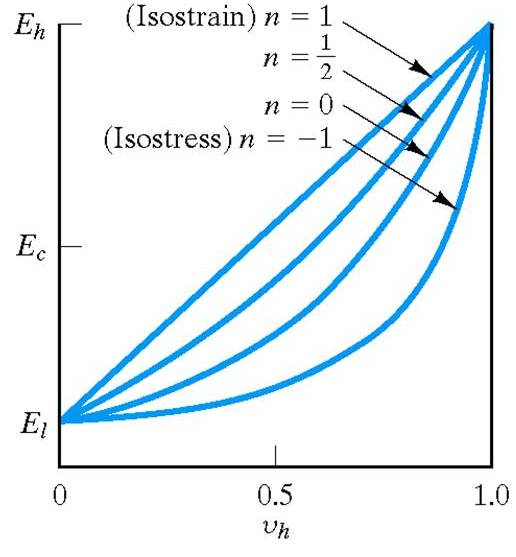
Xcn = Vl Xln + Vh Xhn
Where
- l indicates the low modulus phase
- h indicates the high modulus phase
- n represents different geometries and will range between –1 and +1
In
other words, for any composite, isostrain represents an upper bound and
isostress represents a lower bound for calculating the property of the composite.
Indeed, for aggregate composites,
the dependence of a property on the volume fraction of a
high-modulus phase, Vh, is generally between
the extremes of isostrain and isostress conditions. Decreasing n
from +1 to =1 represents a trend from a relatively low-modulus
aggregate in a relatively high-modulus matrix to the reverse case of a
high-modulus aggregate in a low-modulus matrix.
In summary: To Calculate the Property of a Composite Material
The property of any composite material, Xc, can be calculated from this equation:
Xcn = Vl Xln + Vh Xhn
Where
- l indicates the low modulus phase
- h indicates the high modulus phase
- n represents different geometries and will range between –1 and +1
- n = +1 corresponds to isostrain.
It is also the upper bound for particulate composites. - n = -1 corresponds to isostress.
It is also the lower bound for particulate composites. - n =1/2 corresponds to a relatively low modulus aggregate in a relatively high modulus matrix.
“rubber balls in a steel matrix” - n = 0 corresponds to a high modulus aggregate in a low modulus matrix.
“steel balls in a rubber matrix.”

