Property Averaging for Composites: Isostress

Property Averaging for the Case of Isostress

Calculating Young's Modulus for a Composite Material Under Isostress
Now we will look at the specific case of calculating the modulus of elasticity for transverse loading of a composite material with continuous aligned fibers, i.e. the load is perpendicular to the alignment of the fibers.
This specific case is called isostress since the stress in the fibers and the matrix is the same:

s_c = s_m = s_f= s

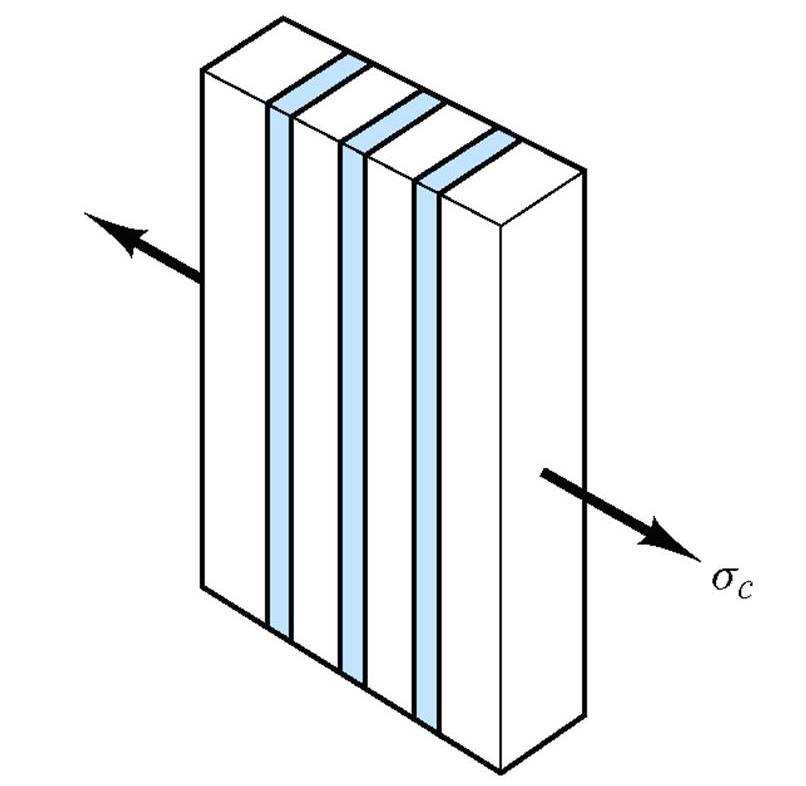
A slab of composite material showing uniaxial loading perpendicular to the fiber reinforcement which has same cross section as composite.

The total elongation of the composite is the sum of the elongation of the fibers plus the elongation of the matrix:

deltaL_c = deltaL_m + deltaL_f

Divide this equation by L_c :

deltaL_c/L_c = deltaL_m/L_c + deltaL_c /L_c

Note:

L_m = (L_ct L_m) / (L_ct)
L_m = L_c (tL_m /tL_c)
L_m = L_cV_m

Solving this for L_c gives:

L_c= L_m/V_m

Similarily we can get:

L_c= L_f/V_f

Substituting into the above equation with these expressions for L_c gives:

deltaL_c/L_c = V_m(deltaL_m/L_m) + V_f (deltaL_f /L_f)

e_c = V_m e_m + V_f e_f

Substituting for the strain, e, using the stress (e = s/E):

(s_c/E_c) = V_m (s_m/E_m) + V_f (s_f/E_f)

And since s_c = s_m= s_f = s, we have finally:

E_c^-1 = V_m E_m^-1 + V_fE_f^-1

Calculating Other Properties for a Composite Material Under Isostress
Although this derivation was for Young's modulus, this relationship holds for many properties.
In general for isostress conditions:

X_c^-1 = V_m X_m^-1 + V_fX_f^-1

where X is:

E, Young’s modulus
D, diffusivity
k, thermal conductivity
sigma, electrical conductivity
nu, poisson’s ratio

PREVIOUS PAGE NEXT PAGE