Property Averaging for the Case of Isostrain
The properties of a composite must, in some way, represent an average of the properties of their individual components. The precise nature of the "average" is a sensitive function of the microstructural geometry.

Calculating Young's Modulus for a Composite Material Under Isostrain
We will look at a specific case of calculating the modulus of elasticity for a composite material with continuous aligned fibers parallel to the loading. This specific case is called isostrain since the strain of the fibers and the matrix is the same:
ec = em = ef = e
This of course assumes that the matrix is intimately bonded with the fibers.
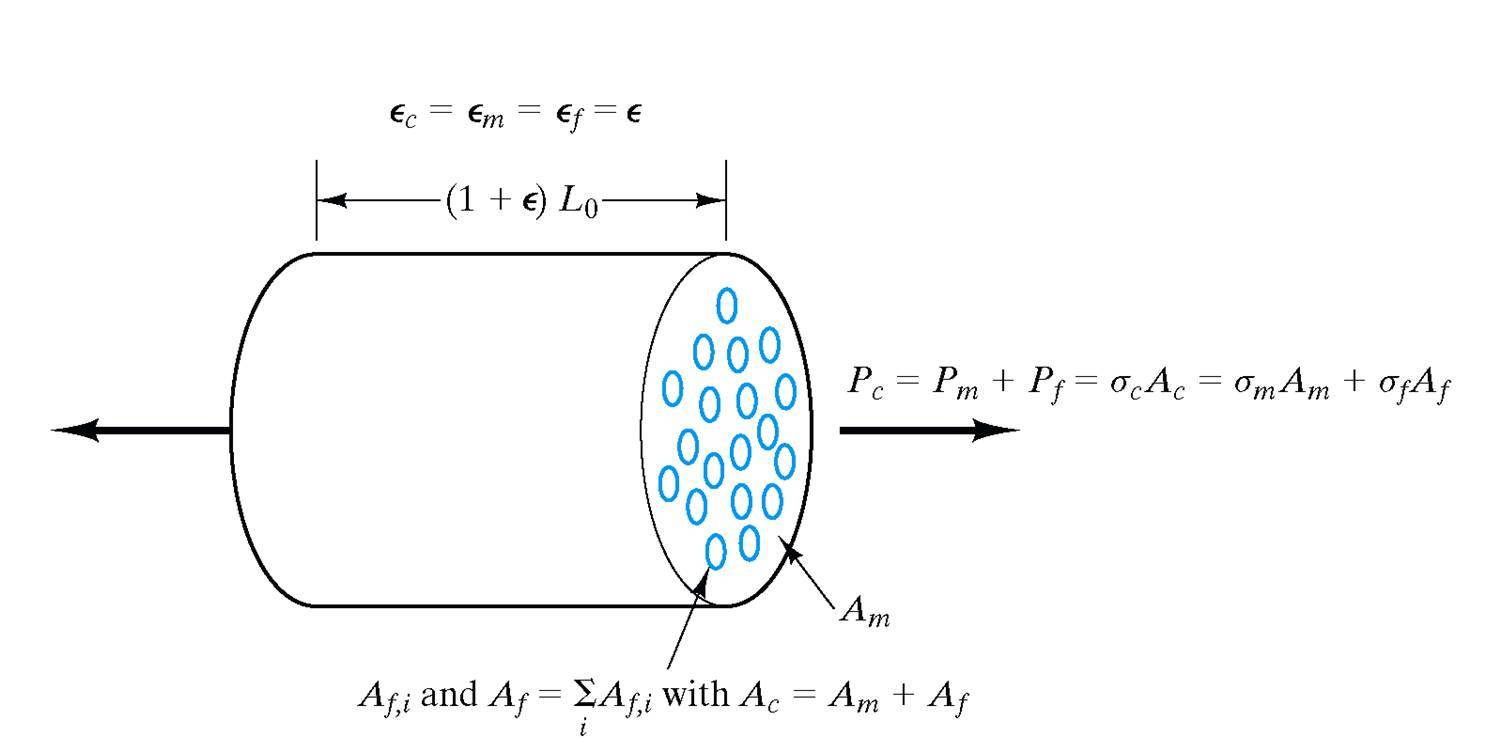
A picture showing uniaxial stressing of a composite with continuous fiber reinforcement. The load is parallel to the fibers.

The load that the composite carries is the sum of the load on the fibers and the load on the matrix:
Pc = Pm + Pf
Substitute an expression for the load, P, using the stress (P = sA):
scAc = smAm + sfAf
Now substitute an expression for the stress, s, using the strain and Young's modulus (s = eE):
ecEcAc  = emEmAm + efEfAf
And since ec = em = ef = e we have:
eEcAc  = eEmAm + eEfAf
Cancelling out the e and solving for Ec gives:
Ec  = (Am/Ac) Em + (Af /Ac)Ef
If Vm & Vf  are volume fractions of matrix and fibers respectively, we finally have our answer:
Ec  = VmEm + VfEf     
So we see that for this case of isostrain conditions, the composite modulus, Ec, is simply the weighted average of the moduli of the components.

Calculating Other Properties for a Composite Material Under Isostrain
Although the above derivation was for Young's modulus, the relationship we obtained holds for many material properties.
In general for isostrain conditions:
Xc  = VmXm + VfXf    
where X is:    
                     
Calculating Fraction of Load Carried by Fibers Under Isostrain 
Let’s also examine the total fraction of the load carried by the fibers:
Pf /Pc  = sfAf/scAc
Pf /Pc  = eEfAf / eEcAc  
Pf /Pc  = (Af/ Ac )(Ef/ Ec)
Pf /Pc  = Vf (Ef / Ec)
               
Since  Ef >> Ec  this can be very effective. It means that the high strength fibers will carry most of the load.  For some fiberglass, the fibers can carry ~96% of the load! The ductile matrix make this a less brittle material.  Hence we get the “best of both worlds”:  strength and ductility!


PREVIOUS PAGE                             NEXT PAGE