Recursion
Contents
Introduction
A recursive function is one that can call itself. Most modern languages support this technique. Many problems in computer science can be solved elegantly using recursion. Many graph , sorting problems can be solved by recursive algorithms.Usually this is when a problem can be broken down into smaller problems that are similar to the original problem. However recursion can place a large burden on resources like the stack than non-recursive ( iterative ) approaches. Even though a recursive approach may express and solve a problem in an elegant manner; the analysis of a recursive algorithm may be prove to be very complex and not that intuitive. Tracing through a recursive algorithm ( line by line ) is not very intuitive and involves keeping track of more things . The recursion technique takes some time to learn and become familiar with.
It is essential that a recursive function have a condition that stops this infinite calling of functions.
File: r1.cpp
#include <iostream> using namespace std ; void recursiveFunction(int noOfTimesToRun) { if ( noOfTimesToRun == 0 ) return ; cout << "Inside the recursive function." << endl ; noOfTimesToRun-- ; recursiveFunction(noOfTimesToRun) ; } int main() { recursiveFunction(5) ; } $ g++ r1.cpp ; ./a.exe Inside the recursive function. Inside the recursive function. Inside the recursive function. Inside the recursive function. Inside the recursive function.Let's examine some simple problems that we can solve using recursion. Many of these problems have simple iterative solutions whereas for others the iterative solutions are not that obvious.
Factorial
FactorialA factorial of a number n is defined as a product of all numbers less than or equal to n. So factorial of 4 is
4*3*2*1 = 24
We also think of the solution as the number 4 multiplied by the factorial of 3 . Also factorial of 0 is 1 and factorial of 1 is 1.
File: f1.cpp
#include <iostream> using namespace std ; int factorial(int number) { int result ; if ( number == 0 || number == 1 ) return 1 ; result = number * factorial( number - 1 ) ; return result ; } int factorialIterative(int number) { int result = 1 ; if( number == 0 ) return 1 ; for( int i1=1 ; i1<=number ; i1++ ) result = result*i1 ; return result ; } int main() { cout << factorial( 4 ) << endl ; cout << factorialIterative( 4 ) << endl ; } $ g++ f1.cpp ; ./a.exe 24 24
Fibonacci Sequence
The Fibonacci Sequence is an addition of the previous 2 numbers with the first two numbers being 0 and 1. The 0th Fibonacci number is 0.// 0 1 1 2 3 5 8
// 0 1 2 3 4
The line:
return fibonacci( nth-1) + fibonacci( nth-2) ;
is basically stating that return the sum of the previous 2 fibonacci numbers.
File: f2.cpp
#include <iostream> #include <stdio.h> #include <string.h> using namespace std ; int fibonacci( int nth ) { if( nth <=0 ) return 0 ; if ( nth == 1 || nth == 2 ) return 1 ; return fibonacci( nth-1) + fibonacci( nth-2) ; } // 0 1 1 2 3 5 8 // 0 1 2 3 4 int main() { cout << fibonacci(4) << endl ; }One way of tracing how a recursion function works is by drawing a tree like diagram.
For fibonacci(4):
fibonacci(4)
fibonacci(3) + fibonacci(2)
fibonacci(2) + fibonacci(1) fibonacci(1) + fibonacci(0)
fibonacci(1)+fibonacci(0)
1 + 0 + 1 1 + 0
2 + 1
=3
Notice that in the diagram above we are calculating some of the numbers
multiple times. We can save the result of a number whose Fibonacci
Exercise:
Write the to do in the below program:
File: ex1.cpp
#include <iostream> #include <stdio.h> #include <string.h> using namespace std ; int powerRecursive( int base, int power ) { //TO DO // base to power = base * base to (power -1 ) return ( 1 ) ; } int powerIterative( int base, int power ) { if ( power == 0 ) return 1 ; if ( power == 1 ) return base ; int result = base ; for(int i1 = 1 ; i1 < power ; i1++ ) { result = result * base ; } return result ; } int main() { cout << powerIterative(2, 4) << endl ; cout << powerRecursive(2, 4) << endl ; }
Reverse an array
File: r2.cpp
#include <iostream> #include <stdio.h> #include <string.h> using namespace std ; void reverse(char array1[] , int leftIndex, int rightIndex ) { char tempChar ; if ( rightIndex <= leftIndex ) return ; tempChar = array1[ leftIndex ] ; array1[ leftIndex ] = array1[ rightIndex ] ; array1[ rightIndex ] = tempChar ; leftIndex++ ; rightIndex-- ; reverse( array1, leftIndex, rightIndex ) ; } int main() { //char ptr[] = "some" ; char ptr[] = "table" ; //char ptr[] = "A string to be reversed." ; reverse( ptr, 0, strlen(ptr) -1 ) ; cout << ptr << endl ; }
Find Prime Factors
The problem is to find out all the prime factors.
File: prime1.cpp
#include <iostream> #include <stdio.h> #include <string.h> using namespace std ; void printPrimeFactors(int num) { static int divisor = 2; // 2 is the first prime number if ( num == 1 ) //if num = 1 we finished { divisor = 2; //restore divisor, so it'll be ready for the next run cout << endl ; return; } else if ( num % divisor == 0 ) //if num divided by divisor { cout << divisor << " "; //print divisor printPrimeFactors( num / divisor ); //call the function with num/divisor } else //if num not divided by divisor { divisor++; //increase divisor printPrimeFactors( num ); } } void printPrimeFactorsIter(int num) { int divisor = 2; // 2 is the first prime number while ( num > 1 ) { if ( num % divisor == 0 ) { cout << divisor << " "; //print divisor num = num / divisor ; } else divisor++ ; } //while cout << endl ; } int main() { int x1 ; cout << "Input number:" ; cin >> x1 ; printPrimeFactors( x1 ) ; printPrimeFactorsIter( x1 ) ; cout << endl ; }
Hanoi Towers
There are 3 poles and disks of varying sizes. Initially the disks are stacked on 1 pole ( we can call it the source ). The problem is to transfer all the disks to another pole ( call it the destination ) so that the destination contains the stack of disks. However when transferring the disks the larger disk cannot be placed on top of a smaller disk.If we play around with this problem we can break the problem down. If we have n disks first move the top n-1 disks to the spare pole and then move the nth ( largest disk) to the destination and then move the n-1 disks from the spare pole to the destination. We can do this easily for 2 disks and the below diagram shows how this is done for 3 disks.
See full image
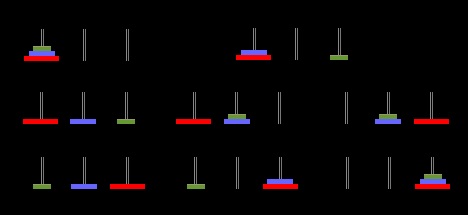
The pseudocode looks something like: MoveTower(disk, source, dest, spare): IF disk == 1, THEN: move disk from source to dest ELSE: MoveTower(disk - 1, source, spare, dest) // Step 1 above move disk from source to dest // Step 2 above MoveTower(disk - 1, spare, dest, source) // Step 3 above END IF
File: hanoi1.cpp
#include <stdio.h> void towers(int num, char frompeg, char topeg, char auxpeg) { // Base Condition if no of disks are if (num == 1) { printf("\n Move disk 1 from peg %c to peg %c", frompeg, topeg); return; } // Recursively calling function twice towers(num - 1, frompeg, auxpeg, topeg); printf("\n Move disk %d from peg %c to peg %c", num, frompeg, topeg); towers(num - 1, auxpeg, topeg, frompeg); } int main() { int num; printf("Enter the number of disks : "); scanf("%d", &num); printf("The sequence of moves involved in the Tower of Hanoi are :\n"); towers(num, 'F', 'T', 'A'); return 0; } $ g++ hanoi1.cpp ; ./a.exe Enter the number of disks : 2 The sequence of moves involved in the Tower of Hanoi are : Move disk 1 from peg F to peg A Move disk 2 from peg F to peg T Move disk 1 from peg A to peg T
Merge Sort
Merge sort divides an array in 2 parts; the 2 parts are then sorted ( recursively ) and then "merged" together. When the array is of size 1 then the array is considered sorted. The below diagram gives and idea of how merge sort works. Merge sort has a feature that initially when the array is divided each part can be sorted independently from the other part. With a bit of modificiation this allows us to sort a very huge file without consuming too much memory.See full image
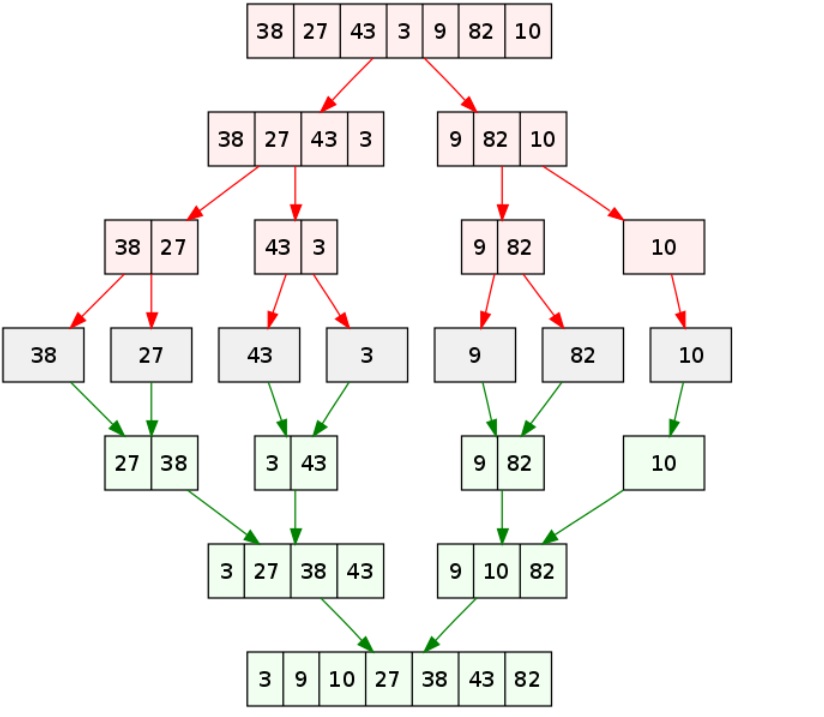
File: merge.cpp
#include<stdlib.h> #include<stdio.h> void printArray(int A[], int size) { int i; for (i=0; i < size; i++) printf("%d ", A[i]); printf("\n"); } // Merges two subarrays of arr[]. // First subarray is arr[l..m] // Second subarray is arr[m+1..r] void merge(int arr[], int left, int middle, int right) { int i1, j1, k1; int n1 = middle - left + 1; int n2 = right - middle ; /* create temp arrays */ int L[n1], R[n2]; /* Copy data to temp arrays L[] and R[] */ for (i1 = 0; i1 < n1; i1++) L[i1] = arr[left + i1]; for (j1 = 0; j1 < n2; j1++) { int index ; index = left ; index = index + middle + j1 ; //((middle+left )+ j1) ; R[j1] = arr[ index ] ; } /* Merge the temp arrays back into arr[l..r]*/ i1 = 0; // Initial index of first subarray j1 = 0; // Initial index of second subarray k1 = left; // Initial index of merged subarray while (i1 < n1 && j1 < n2) { if (L[i1] <= R[j1]) { arr[k1] = L[i1]; i1++; } else { arr[k1] = R[j1]; j1++; } k1++; } /* Copy the remaining elements of L[], if there are any */ while (i1 < n1) { arr[k1] = L[i1]; i1++; k1++; } /* Copy the remaining elements of R[], if there are any */ while (j1 < n2) { arr[k1] = R[j1]; j1++; k1++; } printf( "left:%d middle:%d right:%d\n" , left, middle, right ) ; printArray(arr, 6); } /* l is for left index and r is right index of the sub-array of arr to be sorted */ void mergeSort(int arr[], int left, int right ) { if (left < right ) { // Same as (l+r)/2, but avoids overflow for // large l and h int middle = (left+right)/2 ; // Sort first and second halves mergeSort(arr, left, middle); mergeSort(arr, middle+1, right); merge(arr, left, middle, right); } } int main() { int arr[] = {12, 11, 13, 5, 6, 7}; int arr_size = sizeof(arr)/sizeof(arr[0]); printf("Given array is \n"); printArray(arr, arr_size); mergeSort(arr, 0, arr_size - 1); printf("\nSorted array is \n"); printArray(arr, arr_size); return 0; }
Quick Sort
Quick sort is similiar to merge sort except that the last element is chosen as the pivot point. Elements smaller than the pivot point are placed to the left of this element and elements greater are placed to the right. We now have the pivot element in the right place. The left array of the pivot and the right array of the pivot are unsorted. These 2 subarrays are quick sorted again recursively.See full image
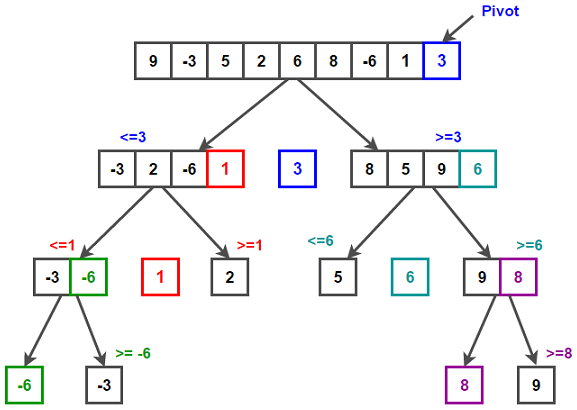
File: quick.cpp
// Quick sort in C++ #include <iostream> using namespace std; // function to swap elements void swap(int *a, int *b) { int t = *a; *a = *b; *b = t; } // function to print the array void printArray(int array[], int size) { int i; for (i = 0; i < size; i++) cout << array[i] << " "; cout << endl; } // function to rearrange array (find the partition point) int partition(int array[], int low, int high) { // select the rightmost element as pivot int pivot = array[high]; // pointer for greater element int i = (low - 1); // traverse each element of the array // compare them with the pivot for (int j = low; j < high; j++) { if (array[j] <= pivot) { // if element smaller than pivot is found // swap it with the greater element pointed by i i++; // swap element at i with element at j swap(&array[i], &array[j]); } } // swap pivot with the greater element at i swap(&array[i + 1], &array[high]); // return the partition point return (i + 1); } void quickSort(int array[], int low, int high) { if (low < high) { // find the pivot element such that // elements smaller than pivot are on left of pivot // elements greater than pivot are on righ of pivot int pi = partition(array, low, high); // recursive call on the left of pivot quickSort(array, low, pi - 1); // recursive call on the right of pivot quickSort(array, pi + 1, high); } } // Driver code int main() { int data[] = {8, 7, 6, 1, 0, 9, 2}; int n = sizeof(data) / sizeof(data[0]); cout << "Unsorted Array: \n"; printArray(data, n); // perform quicksort on data quickSort(data, 0, n - 1); cout << "Sorted array in ascending order: \n"; printArray(data, n); }
Coin change
File: coin.cpp